【機械学習の基本】重回帰分析をPythonで実装してみる

どーも、ぐるたか@guru_takaです。

機械学習の基本である重回帰分析をsklearnで実装し、グラフで色々と可視化してみました！初学者の参考になれば幸いです。

重回帰分析とは？

重回帰分析を簡単にまとめると、単回帰分析の入力変数を１つから複数に拡張したものです。式で表すと、こんな感じ！

$$
y=w_{1} x_{1}+w_{2} x_{2}+\cdots+w_{M} x_{M}+b
$$

最終的に、以下の予測式にある\(\mathbf{w}\)を求めていきます。
$$
\begin{aligned}
y_{q}&=\mathbf{w}^{\mathrm{T}} \mathbf{x}_{q} \\
\mathbf{w}&=\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \mathbf{t}
\end{aligned}
$$

証明といった詳しい解説はこちらの記事をチェックしてみて下さい！上記の式も、こちらの記事を引用しています。
参考 7. 単回帰分析と重回帰分析 — ディープラーニング入門Chainer チュートリアル

単回帰分析については、当ブログの記事も参考にしてみて下さい！

【機械学習の基本】単回帰分析をPythonで実装してみる【numpy, sklearn】

問題設定

sklearnのwineのデータセットを使って、重回帰分析をしていきます！

from sklearn.datasets import load_wine
import pandas as pd

# x:入力変数, t：目的変数
x,t = load_wine(return_X_y=True)

# 入力変数のラベル
labels = load_wine().feature_names

# データフレーム化
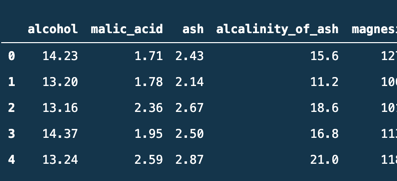
df = pd.DataFrame(data=x, columns=labels)
df.head()

一部のデータですが、こんな風に結果が表示されたらOKです！

標準化

まずはデータを標準化していきます。標準化とは、データを平均0, 標準偏差１にすることをいいます。データのバラツキを統一することで、重み\(w\)の影響度を比較できるようになります。

例えば、家賃を予測することを想定したとき、駅からの距離は1km、治安度は0.1だと、単位も数値の大きさもバラバラになってしまいますよね？なので、標準化が必要なのです。

sklearnには標準化の機能があるので、以下のようにサクッとできちゃいます！

from sklearn.preprocessing import StandardScale

# 標準化
scaler = StandardScaler()
scaler.fit(x)
x_scaler = scaler.transform(x)

# データフレーム化して確認
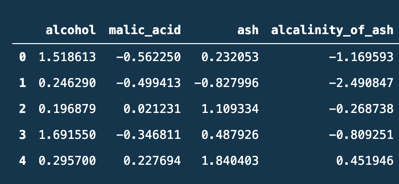
df = pd.DataFrame(data=x_scaler, columns=labels)
df.head()

すると、ちゃんとデータが標準化されているのがわかります！

MEMO

sklearnでの標準化は、不偏標準偏差ではなく母分散を使った標準偏差を使っています!
【Python】Numpy・Pandas・sklearnで標準化する【デフォルトの違いに注意】

下準備は異常です。早速、重回帰分析を実装していきます！

重回帰分析の実装

sklearnでの実装は簡単で、単回帰分析と同じやり方できます！

from sklearn.linear_model import LinearRegression

# モデルの定義
model = LinearRegression()

# モデルの学習
model.fit(x_scaler, t)

これでモデルの学習が完了です！早速、\(x_scaler,t\)の相関関係（決定係数）をみてみましょう。

print('訓練データの相関関係(決定係数) : ', model.score(x_scaler, t))

>>> 訓練データの相関関係（決定係数） :  0.9000888589448974

正の相関が高くて、良い感じです！

せっかくなので、プロットしてみます。

plt.plot(model.predict(x_scaler),'o',label="predict")
plt.plot(t,'o',label='target')
plt.legend()

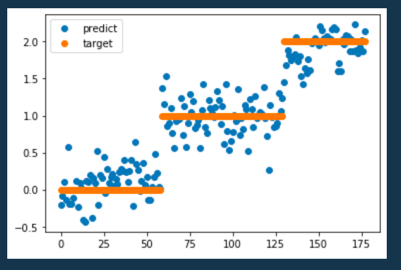
目標値に予測値が群がっている感じがしますね！パラメータも出してみます。

print('重み', model.coef_)
print('バイアス', model.intercept_)

重み [-0.09471963  0.0336106  -0.04063975  0.13272171 -0.00697539  0.09006883
　-0.37092007 -0.03766215  0.02246269  0.17482458 -0.03401722 -0.19119655　-0.2201728 ]

バイアス 0.9382022471910126

最後に、重みの値の比較をしてみます。

plt.bar(x=labels, height=model.coef_)
plt.xticks(rotation=90)
plt.show()

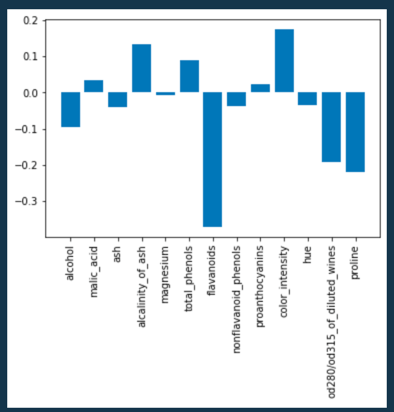
ここからflavonoids（フラボノイドという成分）が大きいと予測値に負の影響を与え、color intensity(濃淡)が大きいと、予測値に正に影響を及ぼすことがわかりす！

参考リンク