どーも、ぐるたか@guru_takaです。
機械学習の基本中の基本である単回帰分析をPythonで実装していきます。初学者の参考になれば幸いです。
MEMO
単回帰分析の証明が気になる方は、こちらの記事を参考にしてみて下さい。わかりやすく、まとめられています!参考 7. 単回帰分析と重回帰分析 — ディープラーニング入門Chainer チュートリアル
問題設定
サンプルデータを使って、15歳の身長を単回帰分析で予測していきます。
サンプルデータは以下のリンクからダウンロードできます!
→samle_height – シート1
| x:年齢 | y:身長 |
| 10 | 140 |
| 12 | 150 |
| 14 | 158 |
| 17 | 170 |
実装例
2つのやり方で進めていきます。
- 自力で計算
- ライブラリ「sklearn」を使用
自力で実装する方法
STEP.1
パッケージインストール
まずは必要なパッケージをインストールします。
python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
STEP.2
データ確認
その後、
pandasを使って、データを読み込みます。 python
# データ読込
df = pd.read_csv('samle_height.csv')
# データ確認
df.head()
すると、ちゃんとデータが表示されます。

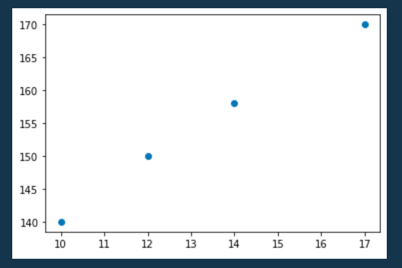
より視覚的にわかりやすくするため、グラフ化すると、こんな風になります。
python
%matplotlib inline
x = df['x']
y = df['y']
plt.plot(x,y,'o')
plt.show()
STEP.3
データの中心化
データの中心化をしていきます。中心化とは、x,yの平均値が(0, 0)になるように、データを平行移動させることを言います。
中心化する理由は、モデル関数\(y=ax+b\)が\(y_c=ax_c\)となり、変数\(b\)がなくなって計算が楽になるからです。
python
# 中心化
x_c = x - x.mean()
y_c = y - y.mean()
# グラフ表示
plt.plot(x_c,y_c,'o')
plt.show()
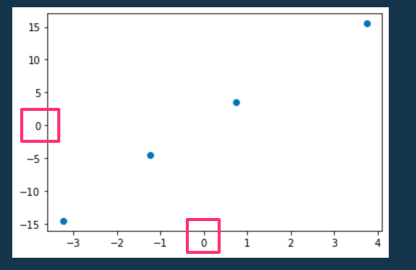
ちゃんと、中心化できたことが確認できました・!
STEP.4
傾きaの算出
続いて、傾き\(a\)(パラメータ)を算出します。算出式は以下の通りです。
$$
a=\frac{\sum_{n=1}^{N} x_{n} y_{n}}{\sum_{n=1}^{N} x_{n}^{2}}
$$
プログラミングで表すと、こうなります!
python
a = sum(x_c * y_c) / sum (x_c * x_c)
a
>> 4.242990654205608
STEP.5
予測
傾き\(a\)が求まったので、予測式を関数化します。
python
def predict(_x):
return a * ((_x) - x.mean()) + y.mean()
中心化したデータを戻すので注意!
実際に予測式をプロットすると、良い感じになります!
python
plt.plot(x,y,'o')
plt.plot(x,predict(x))
plt.show()
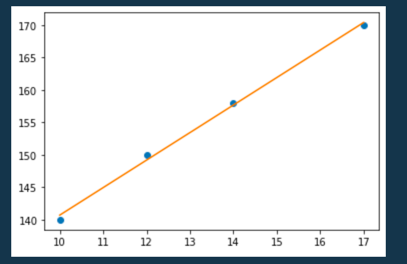
学習用のデータに親しい直線が引かれていることが確認できました!
ライブラリ「sklearn」を使用
ライブラリ「sklearn」を使用すると、もっと簡単に予測式を算出できます。
STEP.1
パッケージインストール
まずは必要なパッケージをインストールします。
python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
STEP.2
データ読込
python
# データ読込
df = pd.read_csv('samle_height.csv')
# 二重括弧にしないと、sklearnで使えないので注意
x = df[['x']]
y = df[['y']]
STEP.3
モデル学習
モデル学習(パラメータ\(a,b\)の算出)も超簡単!
データの中心化を考える必要はなく、コンピュータが良しなにやってくれます。
python
# モデル定義
model = LinearRegression()
# モデル学習
model.fit(x,y)
STEP.4
予測式の確認
最後に学習されたモデル関数(予測式)を確認しましょう!
python
plt.plot(x,y,'o')
plt.plot(x,model.predict(x))
plt.show()

自力で算出した画像と同じです!
パラメータ\(a,b\)の確認方法はこちら!
python
print('a: %.3f' %model.coef_)
print('b: %.3f' %model.intercept_)
>>> a: 4.243
>>> b: 98.280
パラメータ\(a\)が自力で算出した値と同じことがわかります!


コメントを残す